Embarking on a journey of geometric exploration, the Parallel Lines and Transversals Test stands as a cornerstone in understanding the intricate relationships between lines and angles. Delving into this test, we will unravel the fundamental concepts of parallel lines and transversals, uncovering their properties, angle relationships, and theorems.
As we delve deeper into this topic, we will uncover the practical applications of parallel lines and transversals, spanning diverse fields from engineering to architecture. Through engaging examples and illustrative diagrams, we will illuminate the significance of these concepts in shaping our understanding of the world around us.
Defining Parallel Lines and Transversals
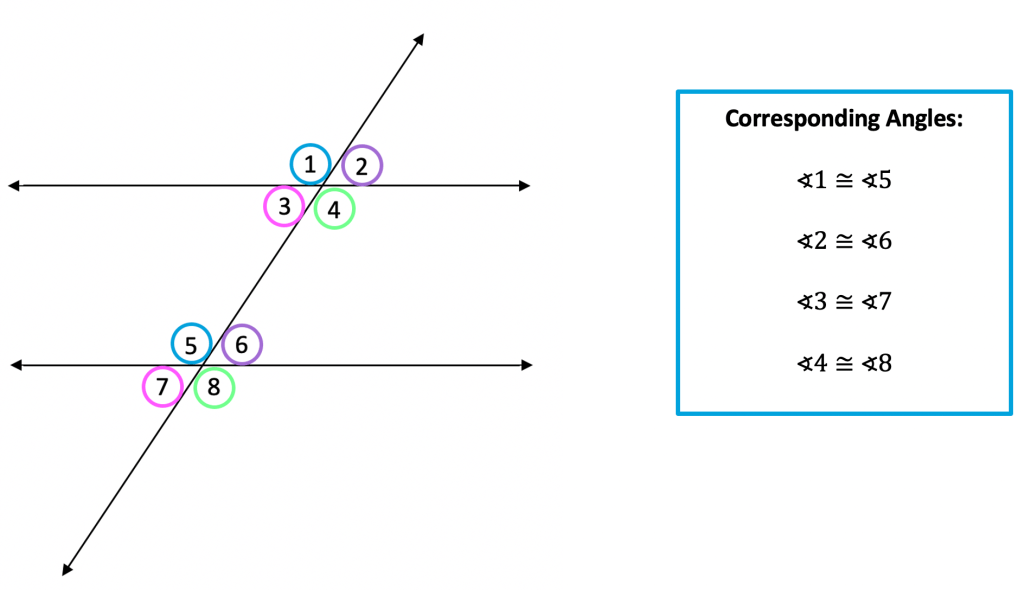
Parallel lines are two lines that never intersect, no matter how far they are extended. Transversals are lines that intersect two or more other lines.
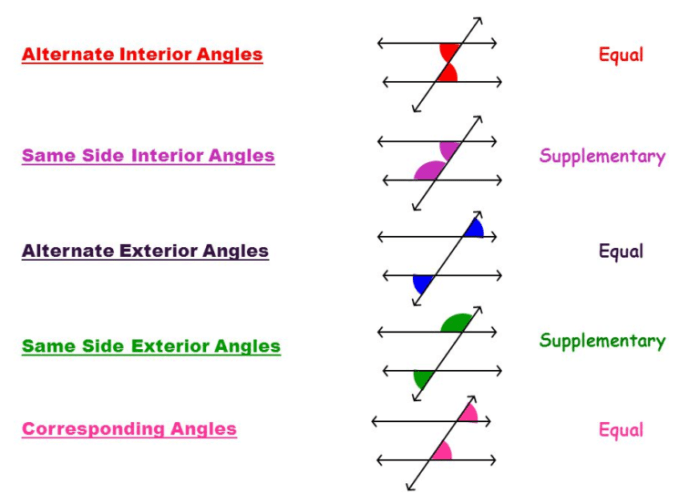
When a transversal intersects two parallel lines, it creates four angles. These angles are called corresponding angles, alternate interior angles, and alternate exterior angles.
The diagram below illustrates the relationship between parallel lines and transversals.

Properties of Parallel Lines and Transversals
There are several properties of parallel lines and transversals. These properties include:
- Corresponding angles are equal.
- Alternate interior angles are equal.
- Alternate exterior angles are equal.
- The sum of the interior angles on the same side of the transversal is 180 degrees.
- The sum of the exterior angles on the same side of the transversal is 360 degrees.
Angle Relationships, Parallel lines and transversals test
The different types of angles formed by parallel lines and transversals are:
- Corresponding angles: These are the angles that are in the same position on both sides of the transversal.
- Alternate interior angles: These are the angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate exterior angles: These are the angles that are on opposite sides of the transversal and outside the parallel lines.
The relationships between these angles are as follows:
- Corresponding angles are equal.
- Alternate interior angles are equal.
- Alternate exterior angles are equal.
Parallel Lines and Transversal Theorems
There are several theorems related to parallel lines and transversals. These theorems include:
- The Converse of the Corresponding Angles Theorem: If two lines are cut by a transversal and the corresponding angles are equal, then the lines are parallel.
- The Converse of the Alternate Interior Angles Theorem: If two lines are cut by a transversal and the alternate interior angles are equal, then the lines are parallel.
- The Converse of the Alternate Exterior Angles Theorem: If two lines are cut by a transversal and the alternate exterior angles are equal, then the lines are parallel.
- The Triangle Sum Theorem: The sum of the interior angles of a triangle is 180 degrees.
- The Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of the opposite interior angles.
Applications of Parallel Lines and Transversals
Parallel lines and transversals have many applications in various fields, including:
- Engineering: Parallel lines are used to create structures that are strong and stable. For example, bridges and buildings are often built using parallel lines.
- Architecture: Parallel lines are used to create buildings that are aesthetically pleasing. For example, the Parthenon in Greece is a temple that is built using parallel lines.
- Everyday life: Parallel lines are used in many everyday objects, such as rulers, pencils, and books.
General Inquiries: Parallel Lines And Transversals Test
What is the definition of parallel lines?
Parallel lines are two lines that never intersect, no matter how far they are extended.
What is a transversal?
A transversal is a line that intersects two or more other lines.
What are the different types of angles formed by parallel lines and transversals?
The different types of angles formed by parallel lines and transversals are alternate interior angles, alternate exterior angles, corresponding angles, and vertical angles.