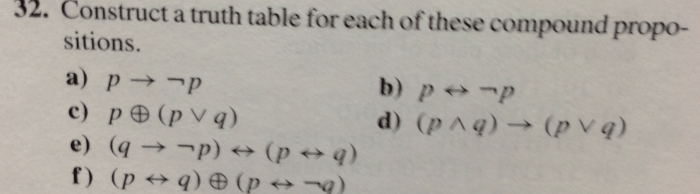Construct a truth table for each of these compound propositions. – Constructing truth tables for compound propositions is a fundamental skill in logic and computer science. By understanding the structure and components of truth tables, we can determine the validity and simplify complex propositions. This comprehensive guide will delve into the purpose, structure, and steps involved in constructing truth tables for compound propositions, providing a solid foundation for further exploration in logic and its applications.
Truth tables provide a systematic way to evaluate the truth value of compound propositions for all possible combinations of their component propositions. They are essential tools for analyzing logical arguments, designing digital circuits, and solving problems in various fields.
Understanding Truth Tables

A truth table is a mathematical tool used to evaluate the truth or falsity of a compound proposition for all possible combinations of its component propositions.
A truth table consists of rows and columns. The rows represent the different combinations of truth values for the component propositions, and the columns represent the truth values of the compound proposition for each combination.
The logical operators used in truth tables are AND, OR, and NOT. The AND operator is represented by the symbol ∧, the OR operator is represented by the symbol ∨, and the NOT operator is represented by the symbol ¬.
Constructing Truth Tables for Compound Propositions
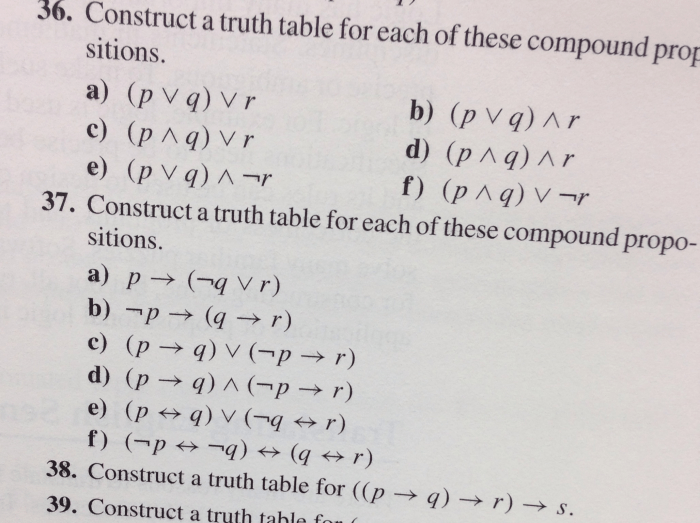
A compound proposition is a proposition that is formed by combining two or more simple propositions using logical operators.
To construct a truth table for a compound proposition, we first need to identify the component propositions and the logical operators that are used to combine them.
Once we have identified the component propositions and the logical operators, we can then create a truth table by listing all of the possible combinations of truth values for the component propositions and the truth values of the compound proposition for each combination.
Examples and Practice
Here is a truth table for a proposition involving the logical operator AND:
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Here is a truth table for a proposition involving the logical operator OR:
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Here is a truth table for a proposition involving the logical operator NOT:
| p | ¬p |
|---|---|
| T | F |
| F | T |
Advanced Applications, Construct a truth table for each of these compound propositions.
Truth tables can be used to determine the validity of arguments.
An argument is valid if and only if the truth value of the conclusion is T for all combinations of truth values for the premises.
Truth tables can also be used to simplify complex propositions.
By using truth tables, we can identify the logical relationships between the component propositions and simplify the proposition into an equivalent proposition that is easier to understand.
Truth tables are also used in computer science and logic.
In computer science, truth tables are used to design and implement digital circuits.
In logic, truth tables are used to study the properties of logical operators and to develop new logical systems.
Commonly Asked Questions: Construct A Truth Table For Each Of These Compound Propositions.
What is the purpose of a truth table?
Truth tables provide a systematic way to determine the truth value of a compound proposition for all possible combinations of its component propositions.
What are the steps involved in constructing a truth table for a compound proposition?
1. Identify the component propositions and their truth values. 2. Create a table with columns for each component proposition and the compound proposition. 3. List all possible combinations of truth values for the component propositions. 4. Use the logical operators (AND, OR, NOT) to determine the truth value of the compound proposition for each combination.
How can truth tables be used to determine the validity of arguments?
Truth tables can be used to determine the validity of arguments by evaluating the truth values of the premises and conclusion for all possible combinations of truth values.